Функция 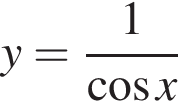 не определена в точке:
не определена в точке:
1) 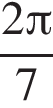
2) 
3) 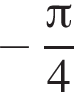
4) 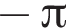
5) 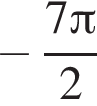
Решение. Функция ![]() не определена, когда
не определена, когда 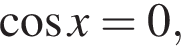 т. е. при
т. е. при 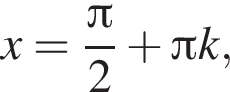 где
где ![]() Таким образом, она не определена в точке
Таким образом, она не определена в точке ![]()
Правильный ответ указан под номером 5.
Ответ: 5
331
5
Сложность: I
Функция 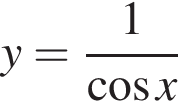 не определена в точке:
не определена в точке:
На клетчатой бумаге с клетками размером 1 см х 1 см изображён параллелограмм. Найдите его площадь в квадратных сантиметрах.
Если 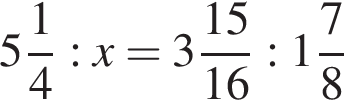 — верная пропорция, то число x равно:
— верная пропорция, то число x равно:
Если 16% некоторого числа равны 24, то 60% этого числа равны:
Если 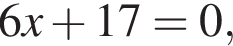 то
то  равно:
равно:
Результат упрощения выражения 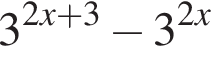 имеет вид:
имеет вид:
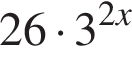
Сумма корней (или корень, если он один) уравнения 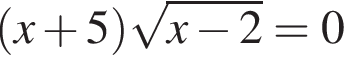 равна:
равна:
От листа жести, имеющего форму квадрата, отрезали прямоугольную полосу шириной 5 дм, после чего площадь оставшейся части листа оказалась равной 24 дм2. Длина стороны квадратного листа (в дециметрах) была равна:
Значение выражения 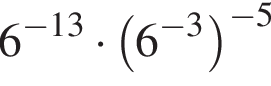 равно:
равно:
Площадь осевого сечения цилиндра равна 32. Площадь его боковой поверхности равна:
Найдите значение выражения 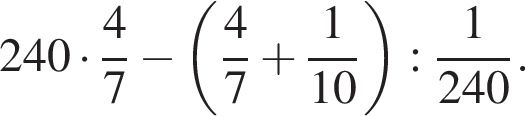
Упростите выражение 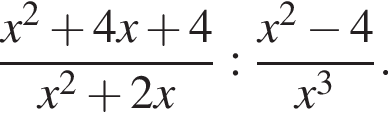
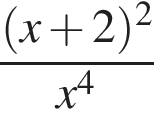
Параллельно стороне треугольника, равной 12, проведена прямая. Длина отрезка этой прямой, заключенного между сторонами треугольника, равна 8. Найдите отношение площади полученной трапеции к площади исходного треугольника.
Сумма координат точки пересечения прямых, заданных уравнениями 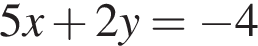 и
и 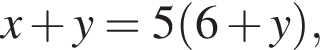 равна:
равна:
Количество целых решений неравенства 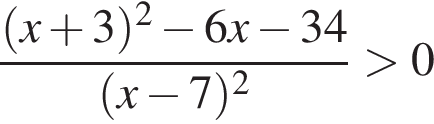 на промежутке
на промежутке 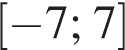 равно:
равно:
В ромб площадью ![]() вписан круг площадью 3π. Сторона ромба равна:
вписан круг площадью 3π. Сторона ромба равна:
Расположите числа 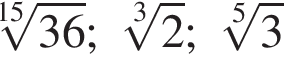 в порядке возрастания.
в порядке возрастания.
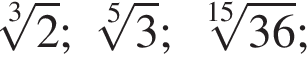
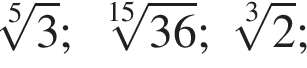
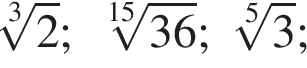
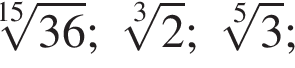
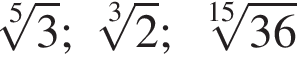
Найдите наименьший положительный корень уравнения 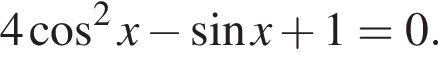

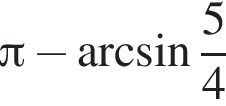
Найдите произведение корней уравнения 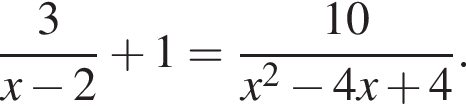
Диагонали трапеции равны 12 и 5. Найдите площадь трапеции, если ее средняя линия равна 6,5.
Сумма корней (или корень, если он один) уравнения 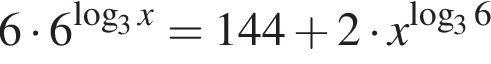 равна ...
равна ...
Найдите сумму целых решений неравенства 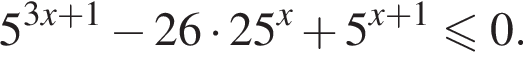
По двум перпендикулярным прямым, которые пересекаются в точке O, движутся две точки M1 и M2 по направлению к точке O со скоростями 1 ![]() и 2
и 2 ![]() соответственно. Достигнув точки O, они продолжают свое движение. В первоначальный момент времени M1O = 1 м, M2O = 17 м. Через сколько секунд расстояние между точками M1 и M2 будет минимальным?
соответственно. Достигнув точки O, они продолжают свое движение. В первоначальный момент времени M1O = 1 м, M2O = 17 м. Через сколько секунд расстояние между точками M1 и M2 будет минимальным?
Найдите
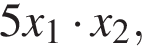 где
где ![]() — абсциссы точек пересечения параболы и горизонтальной прямой (см.рис.).
— абсциссы точек пересечения параболы и горизонтальной прямой (см.рис.).
Четырёхугольник ABCD вписан в окружность. Если 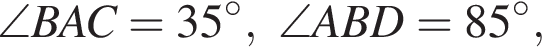 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...
Найдите значение выражения: 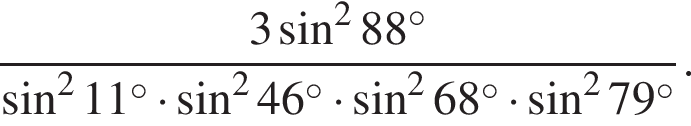
В арифметической прогрессии 120 членов, их сумма равна 120, а сумма членов с четными номерами на 360 больше суммы членов с нечетными номерами. Найдите пятидесятый член этой прогрессии.
В равнобокой трапеции большее основание вдвое больше каждой из остальных сторон и лежит в плоскости α. Боковая сторона образует с плоскостью α угол, синус которого равен ![]() Найдите 45sinβ, где β — угол между диагональю трапеции и плоскостью α.
Найдите 45sinβ, где β — угол между диагональю трапеции и плоскостью α.
Количество целых решений неравенства 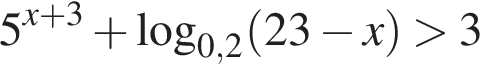 равно ...
равно ...
Основанием пирамиды SABCD является ромб со стороной ![]() и углом BAD, равным
и углом BAD, равным 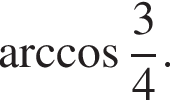 Ребро SD перпендикулярно основанию, а ребро SB образует с основанием угол
Ребро SD перпендикулярно основанию, а ребро SB образует с основанием угол ![]() Найдите радиус R сферы, проходящей через точки A, B, C и середину ребра SB. В ответ запишите значение выражения R2.
Найдите радиус R сферы, проходящей через точки A, B, C и середину ребра SB. В ответ запишите значение выражения R2.